全文线索：

解题引出费波纳茨——>费波纳茨递归解法——>费波纳茨动态规划解法——>矩阵快速幂解法

一、来解题

字符串只由'0'和'1'两种字符构成，当字符串长度为1时，所有可能的字符串为"0"、"1"；当字符串长度为2时，所有可能的字符串为"00"、"01"、"10"、"11"；当字符串长度为3时，所有可能的字符串为"000"、"001"、"010"、"011"、"100"、"101"、"110"、"111"...如果某一个字符串中，只要是出现'0'的位置，左边就靠着'1'，这样的字符串叫作达标字符串。给定一个正数N，返回所有长度为N的字符串中，达标字符串的数量。比如，N=3，返回3，因为只有"101"、"110"、"111"达标。

思路：

对于位置 i，假定 i 前面是1，则 i 有两种情况

当 i=0 时，i+1位必为1，剩下的就是 f(i-2)

当 i=1 时，i+1位可以是1，也可以是0，因此剩下的是 f(i-1)

即f(i)= f(i-2)+ f(i-1) 因此本题可以使用费波纳茨来解。

二、递归解费波纳茨

int process(int i, int n){    if(i==n) return 1;    if(i==n-1) return 2;    return process(i+1, n) + process(i+2, n);}int getNum1(int n){	if(n<1) return 0;	return process(1,n);}int main(){	int n=30;	//普通费波纳茨	int normal=getNum1(n);	cout<
     
      <
     

三、动态规划

int dp(int n){	if(n<1) return 0;	if(n==1) return 1;		vector
     
      num(n+1);	num[1]=1;	num[2]=2;	//第2到第n位的值	for(int i=3; i
     

动态规划空间优化

int dp2(int n){	if(n<1) return 0;	if(n==1) return 1;	int temp=0, cur=1, pre=1;	for(int i=2; i

三、快速幂

铺垫

对于数列 f(n)=f(n-1)+f(n-2)，被减数最大值为2，因此我们的矩阵是2阶的。

数学公式输入不友好，直接上图吧

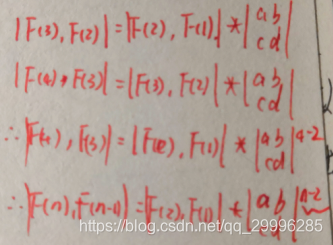
因此可以得到递推式——|f(n)-f(n-1)|=|f(2)-f(1)| * 的（n-2）次幂

a,b,c,d的值需要自行计算。亮点在于高次幂的计算，如何减少高次幂的乘积次数。

先来看看整数高次幂是如何做的

如何提高高次幂运算速度，比如10的75次幂。

第一步：将75拆成二进制，即1001011

第二步：两个辅助变量，t=10，res=1（用于res记录结果）

上伪代码：

int t=10, res=1;vector
     
      flag={1,0,0,1,0,1,1};for(int i=0; i
     

只有二进制位为1的t才会与res进行相乘，时间复杂度为O(logN)

res为10的75次幂的计算结果。

矩阵的高次幂计算同理。

先将（n-2）转成二进制数。上代码：

void turn(int n) {	vector
     
      num;	while (n) {		if (n % 2 == 1)			num.push_back(1);		else			num.push_back(0);		n /= 2;	}}
     

vector中存的是n的二进制，不过是从后往前存的，不过对于从低位到高位依次取出元素来计算，却是方便的（好吧，我就这么村存了，来打我呀）

矩阵乘法

咋算？

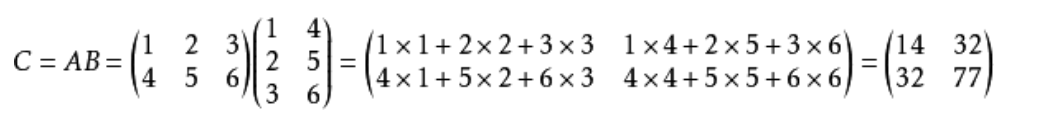
用代码表示矩阵乘法就是玩矩阵了

一步一步来，先看一下矩阵乘法用c++怎么实现（main函数中的m1和m2的位置写反了，见谅）

#include
     
      #include
      
       using namespace std;vector
       
        
         > Matrix_multi(vector
         
          
           >m1, vector
           
            
             >m2){ int temp=0; //m1的行，m2的列，就是结果矩阵的尺寸 vector
             
              
               >res(m1.size(),vector
               
                (m2[0].size())); for(int i=0; i